Ο Ερατοσθένης και το ιστορικό πείραμα

Ή… πώς ο Ερα­το­σθέ­νης μέτρη­σε την ακτί­να της Γης!

Ο Ερα­το­σθέ­νης γεν­νή­θη­κε το 276 π.Χ. στην Κυρή­νεια της Βόρειας Αφρι­κής. Σπού­δα­σε στην Αθή­να από όπου προ­σκλή­θη­κε το 245 π.Χ. από τον Βασι­λέα Πτο­λε­μαίο τον Ευερ­γέ­τη για να ανα­λά­βει τη διεύ­θυν­ση της νεοϊ­δρυ­θεί­σας βιβλιο­θή­κης της Αλε­ξάν­δρειας και την εκπαί­δευ­ση του υιού του Φιλο­πά­το­ρα.

Θεω­ρεί­ται ένας από τους μεγα­λύ­τε­ρους σοφούς της Αρχαιό­τη­τας και θεμε­λιω­τής της Φυσι­κής και Μαθη­μα­τι­κής Γεω­γρα­φί­ας.  Ο σπου­δαί­ος Αρχι­μή­δης τον εκτι­μού­σε ιδιαί­τε­ρα και του αφιέ­ρω­σε το περί­φη­μο έργο του «Περί μηχα­νι­κών θεω­ρη­μά­των προς Ερα­το­σθέ­νη έφο­δος».

Στην Αλε­ξάν­δρεια έζη­σε μέχρι το τέλος της ζωής του το 194 π.Χ.  Λέγε­ται ότι έχα­σε την όρα­ση του και υπέ­βαλ­λε τον εαυ­τό του σε ανα­γκα­στι­κή ασι­τία, που τον οδή­γη­σε στον θάνα­το.

Στο έργο του περι­λαμ­βά­νο­νται μετα­ξύ άλλων η μέτρη­ση της περι­μέ­τρου της γης, η κατάρ­τι­ση κατα­λό­γου αστέ­ρων, η κατάρ­τι­ση χαρ­τών με οικο­νο­μι­κά και εθνο­γρα­φι­κά στοι­χεία, ένα ημε­ρο­λό­γιο, μία μέθο­δος για την εύρε­ση των πρώ­των αριθ­μών γνω­στή ως «Κόσκι­νο του Ερα­το­σθέ­νους», ένα Όργα­νο για τη λύση του προ­βλή­μα­τος του διπλα­σια­σμού του κύβου. Γύρω στο 230 π.Χ. σε έναν πάπυ­ρο της μεγά­λης Βιβλιο­θή­κης της Αλε­ξάν­δρειας, ο Ερα­το­σθέ­νης διά­βα­σε ότι το μεση­μέ­ρι της 21ης Ιου­νί­ου (θερι­νό ηλιο­στά­σιο, η μεγα­λύ­τε­ρη μέρα του τόπου), στα νότια όρια της πόλης Συή­νη (σημε­ρι­νό Ασσουάν), οι κατα­κό­ρυ­φοι στύ­λοι δεν ρίχνουν καθό­λου σκιά και ο Ήλιος καθρε­φτί­ζε­ται ακρι­βώς στον πυθ­μέ­να ενός πηγα­διού (δηλα­δή, βρί­σκε­ται στο Ζενίθ του τόπου). Ως επι­στή­μο­νας διε­ρω­τή­θη­κε εάν συμ­βαί­νει το ίδιο ταυ­τό­χρο­να και σε μια άλλη πόλη πχ. στην Αλε­ξάν­δρεια. Όμως στην Αλε­ξάν­δρεια, που είναι κτι­σμέ­νη στις εκβο­λές του Νεί­λου ποτα­μού βορειό­τε­ρα του Ασσουάν στον ίδιο περί­που μεσημ­βρι­νό, κατά την ίδια μέρα και ώρα, οι κατα­κό­ρυ­φοι στύ­λοι έρι­χναν σκιά.

Αν η Γη ήταν επί­πε­δη, οι κατα­κό­ρυ­φοι στύ­λοι στις δυο πόλεις θα ήταν παράλ­λη­λοι και θα έπρε­πε και οι δυο να ρίχνουν σκιά. Αφού, λοι­πόν, αυτό δεν είναι αλή­θεια, τι μπο­ρεί να συμ­βαί­νει; Την απά­ντη­ση έδω­σε ο Ερα­το­σθέ­νης υπο­στη­ρί­ζο­ντας ότι η επι­φά­νεια της Γης δεν είναι επί­πε­δη αλλά σφαι­ρι­κή. Αυτό το συμπέ­ρα­σμα είναι, προ­φα­νώς, θεμε­λιώ­δους σημα­σί­ας και επι­πλέ­ον επέ­τρε­ψε στον Ερα­το­σθέ­νη να προσ­διο­ρί­σει την ακτί­να και το μήκος της περι­φέ­ρειάς της Γης.

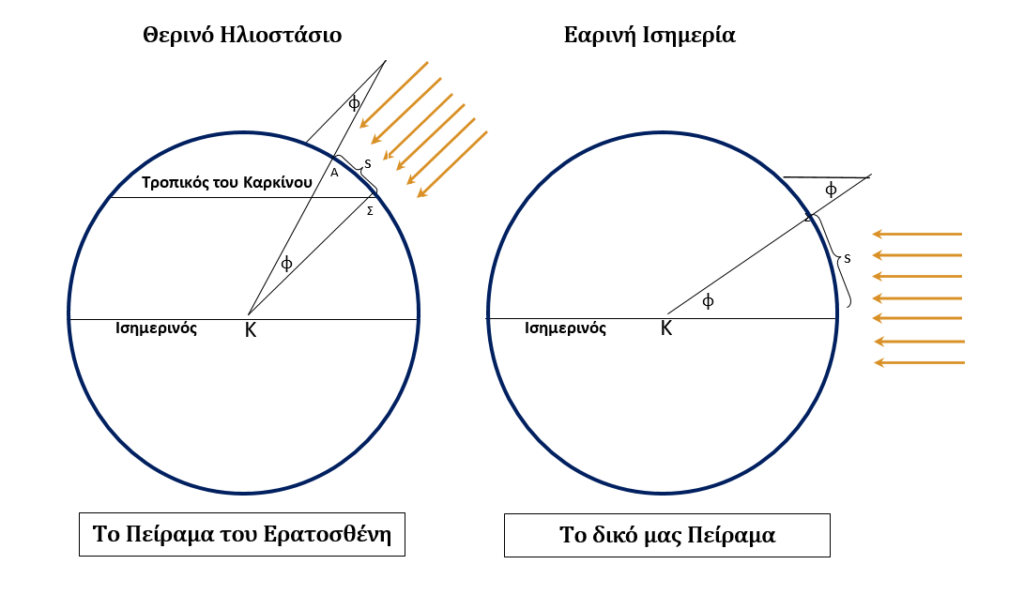
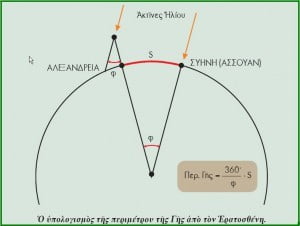Τοπο­θέ­τη­σε έναν κατα­κό­ρυ­φο στύ­λο στην Αλε­ξάν­δρεια την ίδια ακρι­βώς ημέ­ρα και ώρα 12 το μεση­μέ­ρι, μέτρη­σε τη γωνία που σχη­μά­τι­ζε η σκιά του και την βρή­κε ίση με το ένα πεντη­κο­στό της περι­φέ­ρειας κύκλου και λίγο περισ­σό­τε­ρο ακό­μη. Η γωνία ήταν 7,2^ο (περί­που 8 πρώ­τα λεπτά — γωνία φ στο σχή­μα). Αφού η Αλε­ξάν­δρεια και η Συή­νη βρί­σκο­νται πάνω στον ίδιο μεσημ­βρι­νό οι 7,2^ο αντι­στοι­χούν στο ¹⁄₅₀ του πλή­ρη κύκλου (360÷7,2 = 50).

Η από­στα­ση των δύο πόλε­ων ήταν γνω­στή από αφη­γή­σεις βημα­τι­στών και ίση περί­που με 800 Km. Φημο­λο­γεί­ται ότι ο Ερα­το­σθέ­νης μίσθω­σε βημα­τι­στές για τη μέτρη­σή της ή ότι μέτρη­σε αυτήν την από­στα­ση, χρη­σι­μο­ποιώ­ντας ένα είδος οδο­μέ­τρου με γρα­νά­ζια. Εν τέλει η περι­φέ­ρεια της Γης υπο­λο­γί­στη­κε ίση με 40000 Km.

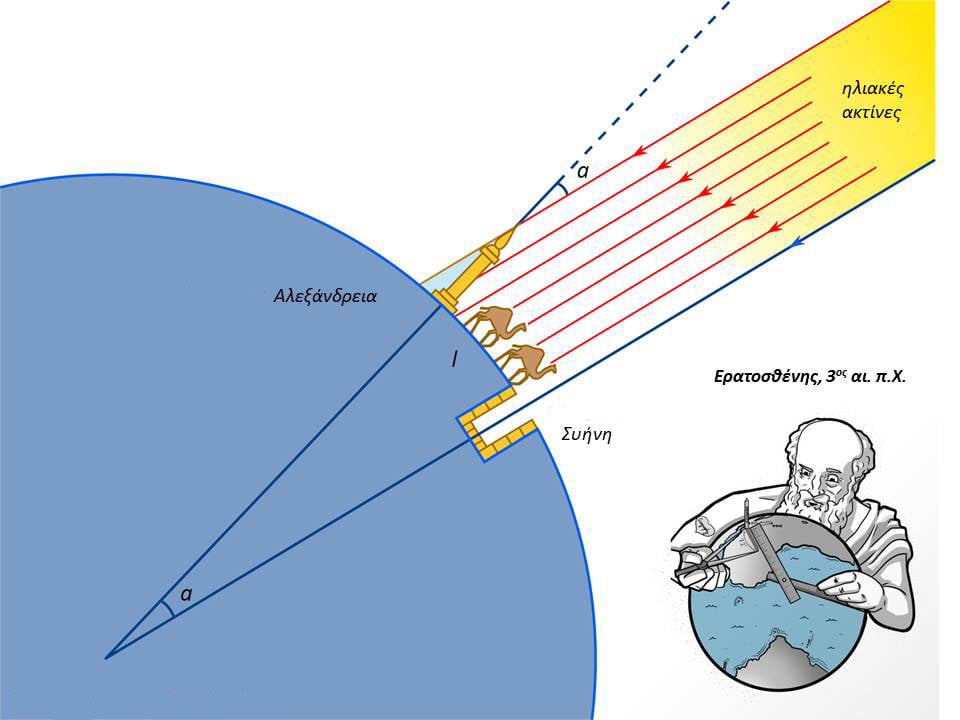
Αυτή είναι η σωστή απά­ντη­ση και ο Ερα­το­σθέ­νης την έδω­σε χρη­σι­μο­ποιώ­ντας ως μόνα εργα­λεία ράβδους, μάτια, πόδια, μυα­λό με απλό­τη­τα σκέ­ψης και επι­νοη­τι­κό­τη­τα. Το λάθος στον υπο­λο­γι­σμό ήταν μόνο 2%, ένα πραγ­μα­τι­κά αξιο­ση­μεί­ω­το επί­τευγ­μα για περί­που πριν από 2,5 χιλιε­τί­ες. Άρα, ο Ερα­το­σθέ­νης ήταν ο πρώ­τος άνθρω­πος που μέτρη­σε τις δια­στά­σεις του πλα­νή­τη Γη, γι’ αυτό και θεω­ρεί­ται δημιουρ­γός της μαθη­μα­τι­κής γεω­γρα­φί­ας.

Εξή­γη­ση του πει­ρά­μα­τος

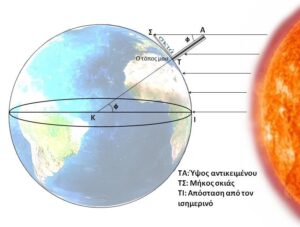Το δικό μας πεί­ρα­μα είναι λίγο δια­φο­ρε­τι­κό αφού θα εργα­στού­με κατά τη διάρ­κεια της εαρι­νής ιση­με­ρί­ας και όχι κατά το θερι­νό ηλιο­στά­σιο, όπως ο Ερα­το­σθέ­νης. Αν θεω­ρή­σου­με ότι ο κύκλος στο διπλα­νό σχή­μα είναι η Γη τότε η έλλει­ψη στο κέντρο είναι ο ιση­με­ρι­νός. Τις ημέ­ρες κοντά στην εαρι­νή ιση­με­ρία, όσοι βρί­σκο­νται στον ιση­με­ρι­νό της Γης θα παρα­τη­ρή­σουν ότι ο Ήλιος το μεση­μέ­ρι βρί­σκε­ται πολύ κοντά στο ζενίθ. Επο­μέ­νως οι ακτί­νες πέφτουν κατα­κό­ρυ­φα και ο Ήλιος θα μπο­ρού­σε να καθρε­φτί­ζε­ται στον πυθ­μέ­να ενός πηγα­διού. Η προ­έ­κτα­ση μιας ακτί­νας του Ήλιου είναι η ΙΚ και περ­νά­ει από το κέντρο της Γης Κ. Έστω ότι εμείς είμα­στε στη θέση Τ. Αν τοπο­θε­τή­σου­με μια κατα­κό­ρυ­φη ράβδο ΤΑ = Υ cm τότε αυτή το μεση­μέ­ρι έχει σκιά ΤΣ = Χ cm.

Υπο­λο­γί­ζου­με την εφα­πτο­μέ­νη της γωνί­ας \( \hat{\phi}= \hat{\Sigma AT} \) από το λόγο Χ/Y και έτσι βρί­σκου­με την γωνία \( \hat{\phi} \) σε μοί­ρες. Επει­δή ο ήλιος βρί­σκε­ται πολύ μακριά από τη Γη, μπο­ρού­με να υπο­θέ­σου­με ότι οι ακτί­νες του είναι παράλ­λη­λες. Η γωνία  είναι ίση με την επί­κε­ντρη γωνία  ως εντός και εναλ­λάξ (όπως φαί­νε­ται στο σχή­μα). Άρα λοι­πόν το γεω­γρα­φι­κό πλά­τος της θέσης μας είναι  μοί­ρες. Εύκο­λα μπο­ρού­με να βρού­με ότι το μήκος του τόξου ΤΙ, η γωνία \( \hat{\phi} \)  και η περί­με­τρος S της Γης συν­δέ­ο­νται με τη σχέ­ση:

$$ \frac{TI}{\hat{\phi}}=\frac{S}{360^{\circ}} $$

συνε­πώς η περί­με­τρος της Γης είναι:

$$ TI={\hat{\phi}}\cdot \frac{S}{360^{\circ}} $$

Η ακτί­να της Γης υπο­λο­γί­ζε­ται εύκο­λα από τη σχέ­ση \( S=2 \pi R \) η οποία δίνει:

$$ R= \frac{S}{2 \pi} $$

Σχε­τι­κή παρου­σί­α­ση

Το πεί­ρα­μα του Ερα­το­σθέ­νη: Φύλ­λα Εργα­σί­ας

Στο φύλ­λα εργα­σί­ας που ακο­λου­θούν περι­λαμ­βά­νο­νται τα βήμα­τα του πει­ρά­μα­τος. Οι πλη­ρο­φο­ρί­ες που περι­λαμ­βά­νο­νται σε αυτά αλλά και στην παρού­σα ανάρ­τη­ση, αντλή­θη­καν από εκπαι­δευ­τι­κό υλι­κό που παρα­χω­ρή­θη­κε από το ΕΚΦΕ Σερ­ρών για την υλο­ποί­η­ση του πει­ρά­μα­τος.

Υπο­λο­γι­στι­κό φύλ­λο (.ods)

Υλο­ποί­η­ση πει­ρά­μα­τος το 2018

Το πεί­ρα­μα του Ερα­το­σθέ­νη: Video

Χρή­σι­μοι Σύν­δε­σμοι

Υδρό­γειος σφαί­ρα
(για την επί­δει­ξη της σφαι­ρι­κό­τη­τας της Γης)

Υλο­ποί­η­ση Πει­ρά­μα­τος
Οι μαθη­τές μετρούν!

Το πεί­ρα­μα για δύο σχο­λεία